Онлайн калькулятор для расчета площади комнаты, стен, потолка и пола в квадратных метрах

Важные моменты, которые нужно учесть перед проведением расчетов

Как посчитать квадратуру крыши дома? Для начала стоит изучить памятку для проведения точных расчетов:

Разделять непрямоугольную кровлю на части сложной конфигурации нужно для упрощения дальнейших расчетов

Этими частями могут быть треугольники, квадраты, прямоугольники и так далее.
Для расчета количества строительного материала, которым будут покрывать крышу важно учесть качество покрытия.
Площадь скатной кровли для покупки мягкого, оцинкованного, шиферного материала можно вычислить по формуле. S = (Ширина свесов x 2 + Длина дома) x (Ширина свесов x 2 + Ширина дома) / cos (Угол наклона).. Если у двухскатной крыши известна ширина одного ската (отрезок от угла крыши до конька) и его длина, применяется простейшая формула для определения площади прямоугольника

А именно: S = A x B. Здесь А – это длина, В – ширина. Полученное значение умножается на два, так как скатов именно два

Если у двухскатной крыши известна ширина одного ската (отрезок от угла крыши до конька) и его длина, применяется простейшая формула для определения площади прямоугольника. А именно: S = A x B. Здесь А – это длина, В – ширина. Полученное значение умножается на два, так как скатов именно два.

Схема расчета двускатной крыши

При разделении крыши сложной формы на несколько более простых фигур и дальнейшем проведении расчетов может пригодиться формула площади прямоугольного треугольника: S = 1/2 x A x B. Тут буквами А и В обозначены катеты, то есть те стороны этой геометрической фигуры, которые прилегают к прямому углу треугольника.

Для расчета площади равнобокой трапеции (если один из скатов крыши имеет правильную трапециевидную форму с одинаковыми по длине боковыми сторонами), кроме ширины ската, нужно знать длину основания трапеции (обычно это длина дома или чуть больше) и ее высоту h (перпендикулярно проведенный отрезок, соединяющий верхушку конька и основание трапециевидного ската): S = (a + b) / 2 x h.

При разделении всей поверхности крыши на разные геометрические фигуры, необходимо вооружиться не только рулеткой для измерения, но и формулами по вычислению площади треугольника, прямоугольника, трапеции и параллелограмма.

Актуальность покрытия крыши

В настоящее время во всем мире, в том числе и в России, бурными темпами развивается такая отрасль народного хозяйства, как строительство. Еще с древних времен этот вид деятельности очень ценился и был востребованным. И по сей день ничего не поменялось. Ежегодно строятся тысячи новых домов, обустраиваются и ремонтируются новые. Особенный интерес к строительству возникает у владельцев частных домов, которые украшают свои владения. Это могут быть небольшие дачи, домики или же большие коттеджи. Один из важных этапов строительства — это покрытие крыши.

Строительство дома никогда не обходится без крыши, поэтому стоит внимательно подойти к проектированию данной части дома, т.к. именно она защищает дом от осадков и других природных воздействий.

Дом, то есть его внешний вид, во многом определяется именно ей. Крышу можно покрывать с помощью различных материалов: шифера, металлочерепицы, металлических листов и так далее. Работа требует точных расчетов материала и необходимых инструментов. Покрыть ее могут и специалисты, и сам хозяин дома, все зависит от желания и навыков. Кроме того, при этом можно сэкономить хорошие деньги. Рассмотрим более подробно, как посчитать площадь этой части дома, ведь это один из основных и самый главный подготовительный этап в ходе работы.

Площадь квадрата

Из известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– ) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это . Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I2<S (случай, когда I2>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его , для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Основные этапы работ

Расчёт площади крыши всегда следует начинать с :

• ознакомления с будущим проектом кровли дома и запоминания наиболее ключевых параметров: длины конька, угла уклона, высоты, ширины и длины;
• определения типа кровельного материала, который будет использоваться.

Одной из самых важных характеристик является специальный расчетный коэффициент, присутствующий абсолютно во всех формулах. Его значение зависит от угла ската крыши и определяется следующими соотношениями :

• при наклоне скатов 9°, коэффициент составит 1,01;
• для 14° – 1,03;
• для 18° – 1, 05;
• при 23° – 1,08;
• при 27° – 1,12;
• для 34° – 1,2.

Еще несколько советов

Прежде чем посчитать квадратуру жилого пространства, возьмите на заметку несколько важных нюансов:

• Основной единицей измерения S являются квадратные метры;
• Если оконный, или дверной проем в стене, почти всегда можно измерить за 1 раз, то в случае с полом и потолком все действия проходят в определенной последовательности. Разложите рулетку, сделайте отметку там, где она закончилась, потом снова приложите ее к обозначенной точке и продолжите измерения. Делайте так до тех пор, пока не измерите всю длину, а затем сложите полученные измерения;
• Если полученная длина составляет больше 1 м, то считать нужно и сантиметры, и метры;
• Длину стены лучше измерять по плинтусу. Для удобства воспользуйтесь помощью напарника;
• Вычисляя квадратные метры пола, стен или потолка, будьте предельно внимательным. Если вы пользуетесь обычной рулеткой, проследите за тем, чтобы она была ровной, а фиксатор не сползал с точки отсчета. В случае с лазерным инструментом убедитесь в том, что луч расположен перпендикулярно стене – в противном случае погрешность в результатах будет слишком большой;
• Как посчитать площадь комнаты, если ее длина составляет чуть больше 1 м? При выполнении таких подсчетов округлите полученное число до ближайшего сантиметра, а миллиметры оставьте;
• Обязательно переведите сантиметры в метры. 1 см = 0,01 м, поэтому для перевода достаточно переставить запятую на 2 цифры влево (например: 2 м 35 см = 2,35 м, 8 см = 0,08 м);
• Чтобы получить максимально точные показатели, измеряйте высоту стены в 3 местах — в начале, конце и посредине. Если полученные цифры будут слегка отличаться (так часто бывает в старых постройках), берите среднее арифметическое (К + T + M / 3);
• При определенных расчетах нужно предоставить объем комнаты (так называемую кубатуру). Чтобы узнать эту величину, достаточно перемножить ширину, длину и высоту помещения;
• Тем, кто не уверен в правильности своих подсчетов, советуем воспользоваться онлайн калькулятором;
• При планировании покупок нужно учитывать не только размеры данного помещения, но и особенности применения тех или иных строительных материалов. Это позволит избежать большого количества отходов.

Как видите, в нахождении площади того или иного помещения нет абсолютно ничего сложного. Главное — не спешить и оставаться предельно внимательным. Удачи вам в подсчетах!

Мне нравится1Не нравится

Читайте далее:

Расчет гипсокартона для стен: калькулятор, формулы

Как сделать расчет рулонов обоев, точный калькулятор расчета

Расход затирки для плитки на 1 м² — калькулятор, формула расчета

Расчет гипсокартона на перегородку — нормы расхода, калькулятор

Калькулятор расчета базового обмена веществ, самые точные формулы BMR

Калькулятор расчета гипсокартона на потолок

Калькулятор расчета количества плитки для отделки ванной комнаты

Отделка стен и пола керамической плиткой – лучшее, пожалуй, решение для ванной комнаты. При правильной укладке, такому покрытию не страшны ни повышенная влажность, ни прямое попадание воды, а богатое разнообразие размеров, расцветок, фактур кафеля дают возможность воплотить в жизнь самые смелые дизайнерские фантазии хозяев.

Калькулятор расчета количества плитки для отделки ванной комнаты

Задумывая ремонт в ванной, хозяева обязательно начнут просчитывать, чего и сколько им понадобится. Попробуем несколько облегчить им задачу – для этого ниже размещен калькулятор расчета количества плитки для отделки ванной комнаты. Наверняка, по работе с ним могут возникнуть некоторые вопросы, поэтому сразу под калькулятором, в текстовом блоке, будут приведены необходимые пояснения.

Пояснения по проведению расчетов

Калькулятор универсален, то есть позволяет оценить количество необходимого материала для полной отделки ванной комнаты – ее стен и потолка.

• Прежде всего, необходимо будет внести длину и ширину помещения – эти параметры необходимы для любого из направления расчета.
• Далее, будет предложено выбрать, в какую сторону направить расчёт – произвести вычисления количества плитки для отделки пола или для стен. В соответствии с выбором появятся необходимые поля для ввода данных.

А. Расчет для пола

• Здесь несколько проще – площадь пола вычисляется по указанным выше размерам, а ввести будет необходимо лишь параметры выбранной керамической плитки – ее длину и ширину.
• Кроме того, следует указать и планируемый межплиточный шов – его толщину. Может показаться, что это мелочь, но при больших площадях, а тем более – если используется малоформатная плитка¸ такой параметр может существенно изменить общее количество необходимого материала. В этом можно убедиться, попробовав варьировать толщину шва – насколько поменяется итоговое количество плитки.
• Далее, указывается выбранный принцип укладки – будут ли это традиционные ряды, параллельные и перпендикулярные стенам, или же они расположатся по диагонали. Безусловно, общая площадь покрытия при этом не меняется, но при раскрое кафеля отходов может быть больше. Если для «классической» кладки обычно делается запас керамической плитки в 10%, то для диагональной необходимо сделать резерв больше – 15%. Оба этих параметра уже учтены в программе калькулятора, то есть итоговый результат показывает количество плиток с уже предусмотренным запасом.

Б. Расчет для стен

• Для определения площади стен, помимо уже указанных длины и ширину ванной комнаты, необходимо ввести еще и высоту. Здесь необходимо правильно представлять, что имеется в виду необязательно полная высота стены – нередко отделка делается только до какого-то уровня. Практикуется и использование двух типов плиток, например, более темная нижняя часть стены, и более светлая, «легкая» – верхняя. Таким образом, корректнее будет говорить о высоте отделываемого участка.
• Если стена вся отделывается одним типом плитки, но предполагается вставка горизонтальной полосы-фриза, то можно учесть и его: фриз, особенно если он достаточно «широкий», уменьшит общую площадь покрытия и, стало быть, количество плитки. По умолчанию в слайдере установки ширины фриза стоит «0», то есть если его не будет или толщина его столь мала, что можно не принимать в расчет, то это поле можно просто проигнорировать.
• Из общей площади стен можно вычесть не заполняемые плиткой дверные проемы, окна, другие участки, например, для вмуровывания зеркала, установки дверцы или экрана, закрывающего трубы и т.п. Необходимо будет указать количество таких участков и их габариты.

Здесь также есть нюанс: высоту двери или окна иногда приходится вносить не полную, а только лишь приходящуюся на подлежащий облицовке керамической плиткой участок (по аналогии с высотой отделываемой стены).

• Дальше – все как при расчетах для пола: размеры плитки и планируемая толщина швов.
• Так как на стенах диагональная укладка практикуется нечасто, этот параметр в данном варианте расчета не показан. Результат, выдаваемый калькулятором, также учитывает 10-процентный запас материала.

Площадь стен со сложной поверхностью

Нередко в помещениях много разных элементов, которые усложняют подсчет площади. Так что если стены не прямоугольные или есть разные дополнительные детали, необходимо воспользоваться иным способом расчета площади дома.

1. Площадь стен дома с вычетом дверей и окон.

Двери и окна обычно вычитают из общей площади, потому что на них не идет расход материала. Но как посчитать площадь стен без них?

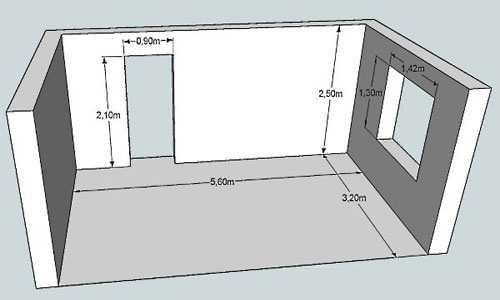
Для начала замеряется ширина и высота окон и дверей.

Формула для площади поверхности – S = a x h.

Если ширина окна 1 м, а высота 1,5 м, то S = 1 х 1,5 = 1,5 м².  При ширине двери 0,9 м и высоте в 2 м получаем S = 0,9 х 2 = 1,8 м². Теперь нужно отнять от общей площади, площадь окон, дверей и получается площадь без них. То есть,

S стен = 66 – 1,5 – 1,8 = 62,7 м² (если использовать площадь стен, полученную в предыдущем пункте).

1. Если комната нестандартной конструкции.

Когда помещение имеет нестандартную форму, расчет площади стен проводится немного иначе. Сначала считается площадь каждой стены в отдельности.

S = a x b, где, а – ширина стены, b – высота стены.

Если есть колонны, выступы, их площадь также измеряется, а затем все эти площади суммируются. То есть, итоговая формула это S = S1 + S2 + S3 + S4 и т. д.

Важно!
В редких случаях геометрические параметры стен абсолютно правильные. Так что для наиболее точных расчетов стоит делать измерения в нескольких местах, а потом выводить среднее арифметическое число и уже его использовать в формулах.

1. Если имеются круглые элементы в архитектуре.

Помещения с круглыми или полукруглыми стенами это не редкость. Чтобы просчитать их площадь используется другая формула. Первым делом вымеряется их периметр. Для этого нужно умножить диаметр на 3,14 (число Пи, π). А затем уже подсчитывается и площадь по формуле:

S = P x h, где, h – это высота.

Когда нужно вычесть из общей квадратуры площадь круглых объектов, нужно рассчитать площадь круглых поверхностей и просто отнять их. Но, если нет возможности вымерять диаметр или радиус, то вымеряют длину окружности (P) и считают площадь, применяя формулу S = P² / 4 π.

1. Площадь с треугольными элементами.

Треугольные стены могут быть, к примеру, на чердаке или в случае, когда используются сложные конструкции на потолке или архитектурные украшения на стенах. В зависимости от типа треугольника использовать можно разные формулы.

• Разносторонний треугольник: S = , где, а – основа треугольника – нижняя сторона, а h – высота от пола к верхнему углу.
• Прямоугольный треугольник: S = , где, а – высота треугольника, а b – нижняя, горизонтальная сторона.
• Равносторонний треугольник (правильный): S = , где, а – сторона треугольника.

Преимущества использования сервиса

Рассчитать количество ламината на комнату на калькуляторе – это удобно, просто и доступно с любого устройства. Результаты вычислений позволяют составить точную смету на будущий ремонт, избежать перерасхода или напротив, столкнуться в самый ответственный момент с недостатком изделий. После ввода в поля программы базовых параметров моментально выдаётся результат, который включает:

• площадь помещения в метрах квадратных;
• количество ламинированных досок, которые будут использованы целиком в ремонте;
• общее количество товара, которого необходимо приобрести;
• расход последней доски (отпил) в миллиметрах;
• количество и ширина обрезков;
• количество упаковок ламината;
• остатки плашек.

Учёт в программе мельчайших нюансов укладки становится залогом грамотной и выгодной закупки материалов.

На простом примере можно предварительно оценить преимущества автоматического расчёта, сравнив результаты программы и самостоятельных вычислений:

• ширина комнаты составляет 4 метров;
• длина — 5 метров;
• характеристики ламината стандартные (Д*Ш) – 1380*156;
• изделий в упаковке — 8 штук;
• схема укладки — по длине комнаты.

Результат показывает, что необходимо приобрести 12 упаковок ламината. При этом остаток будет нулевым, отпил последней плашки – 10.4 см, общее количество доски – 96 штук. Точно таким же образом можно проверить расход материалов при монтаже ламината по ширине комнаты. Самостоятельно считать несложно, но процесс занимает сложное время. Сайт выдаёт результат моментально, без особых усилий со стороны пользователя. Это даёт возможность за минуты просчитать количество материала на все комнаты дома или квартиры, где планируется обновить напольное покрытие.

Применение

Может применяться в расчётах других видов напольных покрытий:

• паркет – классический пол с высокими прочностными характеристиками;
• массива дерева – качественный и надёжный пол с неограниченным сроком эксплуатации;
• пробковое покрытие – экологически чистый материал, собирается как паркетная доска или монтируется на клей;
• модульные ПВХ-покрытия – износостойкий и долговечный материал с минимальными отходами при укладке;
• керамическая плитка для пола – оптимальный вариант напольного покрытия для помещений с повышенной влажностью (ванная, кухня, коридор, лоджия);
• керамогранит – материал с высокой плотностью, обладает исключительными качественными и прочностными характеристиками.

Каждая партия товаров из одной коллекции незначительно отличается по цвету и текстуре, особенно, когда речь идёт о натуральном полотне. Избежать стрессовых ситуаций можно и нужно. Всем перечисленным видам напольного покрытия характерны небольшие размеры составных частей и строго определенное количество в упаковке.

Современные способы подсчёта строительных материалов для ремонта помещений любого назначения существенно экономят время и семейный бюджет. При условии правильного измерения площади квартиры, дома или офиса, риск приобрести лишние метры напольного покрытия сведён к нулю.