Значение тату треугольник: какой рисунок правильно выбрать для нанесения на тело

Женское тату роза в треугольнике: красивые варианты

Очень часто девушки выбирают для себя изображение в виде треугольника, заполненного цветочными мотивами. Розы – самое распространенное из них

С помощью татуировки роз в треугольнике девушка привлекает к себе внимание. Данная нательная композиция прекрасно смотрится как в маленьком, так и большом формате

Место для расположения татуировки треугольника с розами могут быть самыми различными. Все зависит от выбранного размера. Вообще, значение комбинации треугольника с розой трактуется как женская энергетика. Представительницы прекрасного пола, на теле которых можно увидеть тату с розой в комбинации с треугольником, отличаются особым отношением к художественному искусству, музыке и творчеству в целом.

Глаз в треугольнике

Символ, графически представляющий собой вписанный в треугольник глаз, называемый «глазом провидения» или «всевидящим оком», появился в Европе в XVII в. Считается, что он восходит к солярному глазу Гора древних египтян. Этот знак получил широкое распространение в барочной архитектуре, украшая фронтоны роскошных католических костелов.

В XIX в. он появился и на православных храмах, например, на фронтоне Казанского собора в Санкт-Петербурге. Христианство рассматривало его как символ Святой Троицы. Одновременно этот символ использовался и масонами, которые трактовали его как символ абсолюта, просвещения и высшего знания. У масонов «глаз провидения» располагается над стулом мастера ложи, чтобы таким образом напоминать о всепроникающей во все тайны мудрости Творца.

Декларация прав человека и гражданина, Франция, конец XVIII в.

Герб белорусского города Браслав

Второй признак равенства треугольников

Теорема 2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то эти треугольники равны.

Доказательство. Рассмотрим треугольники ABC и A₁B₁С₁ (Рис.4). Пусть AB=A₁B₁, ∠A=∠A₁, ∠B=∠B₁. Докажем, что .

Наложим треугольник ABC на треугольник A₁B₁С₁ так, чтобы вершина A совмещалась с вершиной A₁, сторона AB − со стороной A₁B₁ (по условию теоремы AB=A₁B₁), а вершины C и С₁ оказались по одну сторону от прямой A₁B₁.

Так как ∠A=∠A₁ и ∠B=∠B₁, то сторона AС наложится на луч A₁C₁ а сторона BС − на луч B₁С₁. Тогда вершина C окажется на луче A₁C₁ и на луче B₁C₁. Т.е. она окажется на пересечении этих лучей и, следовательно, вершина C совместится с общей точкой лучей A₁C₁ и B₁C₁, т.е. с вершиной C₁. Таким образом совместятся стороны AC и A₁C₁, BC и B₁C₁. То есть треугольники ABC и A₁B₁С₁ полностью совместятся, поэтому они равны. Теорема доказана.

Формулы прямоугольного треугольника:

Пусть a и b – длины катетов прямоугольного треугольника, с – длина гипотенузы прямоугольного треугольника, h – высота прямоугольного треугольника, проведенная к гипотенузе (АН), R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 9, 11, 12).

Формулы сторон прямоугольного треугольника (a, b, c) по теореме Пифагора:

c​2​​ = a​2​​ + b​2​​ ,

a​2​​ = c​2​​ – b​2​​ ,

b​2​​ = c​2 – a​2 ​​.

Формула радиуса вписанной окружности (r):

 .

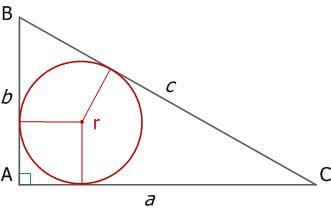
Рис. 12. Прямоугольный треугольник и вписанная окружность

Формула радиуса описанной окружности (R): 

.

Формулы площади (S) прямоугольного треугольника: 

 .

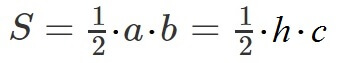Формулы высоты (h)прямоугольного треугольника:

.

Примечание:  Фото https://www.pexels.com, https://pixabay.com

карта сайта

Коэффициент востребованности
15 795

Египетский треугольник в строительстве. Общие сведения

Зарождение идеи

Надо заметить, что более двух с половиной тысяч лет назад пирамиды были несколько другими – огромными, с четкими гранями. Тщательно изучив могущественные постройки, коих было не мало, так как рядом с великанами, стояли храмы поменьше, построенные для детей, жен и других родственных лиц фараона, это натолкнуло его на мысль.

Благодаря своим математическим способностям, Пифагор сумел определить закономерность в формах пирамиды, а умение анализировать и делать выводы привели к созданию одной из самых значимых теорий в истории геометрии.

Из истории

Знали ли в древнем Египте о геометрии и математике? Конечно да. Жизнь египтян была тесно связана с наукой. Они регулярно пользовались знаниями при разметке полей, создании архитектурных шедевров. Даже существовала своя служба землемеров, которые применяли геометрические правила, занимаясь восстановлением границ.

Название треугольник получил благодаря эллинам, которые нередко бывали в Египте в VII-V вв. до н.э. Считается, что прообразом фигуры стала пирамида Хеопса, отличающаяся совершенными пропорциями. Ее место особенное в истории. Если посмотреть поперечное сечение, то можно отметить два треугольника, у которых угол внутри равняется 51о50’.

Строение

Сегодня это строение усеченной формы, приобретенной под воздействием времени, высота явно потерялась. Однако, восстановив ее геометричность, можно сделать вывод, что стороны треугольников равны. Получается в основе заложен золотой прямоугольный треугольник.

Однако, следует рассмотреть другую пирамиду – Хефрена, у которой основа как раз-таки прямоугольный треугольник и где угол наклона боковых граней равен 53о12 с соотношением катетов 4:3. Это уже так называемый священный треугольник. Для египтян такая фигура сопоставлялась с семейным очагом: катет вертикального положения олицетворял мужчину, основание – представительницу прекрасного пола, а гипотенуза – рождение ребенка от обоих.

Стороны пирамиды Хефрена в соотношении равны 3:4:5, что точно соответствует теореме Пифагора. Значит, можно сделать вывод, что строители уже знали об этой теореме, но не могли ее сформулировать. Хотя, в исторических письменах встречаются следы использования египетского треугольника за много веков даже до Египта. До сегодняшнего дня это загадка, как могли такие знания получить древние египтяне. Понимали ли они чем обладают?

Особенность фигуры к тому же в том, что благодаря подобному соотношению, она является простым и первым Героновым треугольником, так как ее стороны и площадь целочисленные.

Обратное доказательство

Таким образом теорема Пифагора стала каноном и фундаментом развития математической науки. Со школьной скамьи каждый ученик знает, что означает выражение «Пифагоровы штаны во все стороны равны».

Интересно, что теорема Пифагора находится в Книге Гиннесса как теорема, обладающая самым большим количеством доказательств, которых примерно 500.

Особенности

Если рассмотреть более детально отличительные особенности египетского треугольника, то можно выделить следующие моменты:

• все стороны и площадь состоят из целых чисел, как говорилось выше;
• согласно теории великого математика, сумма квадратов катетов равна квадрату гипотенузе;
• такой фигурой возможно отмерить прямые углы в пространстве. Это используется в процессе строительства до сих пор;
• не обязательно пользоваться специальными измерительными приборами, подойдут подручные средства, например, веревка.

Фигура треугольник в трейдинге

Теперь, когда мы обсудили большинство важных моделей треугольников, посмотрим, как их можно использовать в своей торговле.

На графике показаны пять примеров треугольников и их потенциальные результаты.

График начинается с большого симметричного треугольника. Цена создает три убывающие вершины и три увеличивающиеся основания на графике. Стрелка в начале треугольника измеряет его размер. Как видите, такая же стрелка применяется, когда цена преодолевает верхний уровень треугольника и указывает на потенциальную цель модели, которая фиксируется через неделю.

Между тем, на пути к повышению цены создается график восходящего клина. Как мы уже говорили, восходящий клин имеет медвежий потенциал. При пробое нижнего уровня клина мы замечаем небольшую коррекцию.

В конце бычьей тенденции цена создает еще один симметричный треугольник. Позже цена пробивает нижний уровень и завершает размер фигуры.

При снижении цены возникает медвежий вымпел. Это консолидация после первого импульса медвежьего тренда. Далее цена пробивает нижний уровень вымпела. На пути вниз мы видим, что цена завершает первую цель, которая равна размеру вымпела.

Затем цена создает модель разворота с двойным дном и переключается на бычье направление. На пути вверх ценовое действие возникает расширяющийся треугольник

Обратите внимание, что верхний и нижний уровни шаблона увеличиваются. В этом случае ожидаемое движение цены является медвежьим и должно быть равным размеру паттерна

Описание линий

Узоры на наших руках – судьба. Есть немало версий и легенд. Утверждают, что будущее зависит от мыслительных процессов, в результате чего вырисовываются линии.

Судьбоносный треугольник

О чем расскажут обе ладони?

1. Интересно, что на левой руке заложены все ресурсы, предназначенные человеку с рождения.
2. Рисунки на правой руке формируются от поступков человека и его самостоятельных решений.
3. Иногда некоторые линии на руке и треугольник присутствуют только на левой руке. Это говорит о том, что человек ещё не использовал свой потенциал.
4. Если фигура находится на правой руке, значит такой представитель – сильная и целеустремлённая личность, способная вносить коррективы в свою судьбу.

На нити жизни

По линии жизни говорят о длительности проживания, о силе и выносливости человека и его внутренних ресурсах.

Жизненный треугольник

На сердечной черте

Линия сердца определяет насколько человек любвеобилен или холоден в эмоциональной сфере. Линия Судьбы указывает какой путь ждёт человека.

Сердечный треугольник

На линии головы

Умственная линия расскажет о способностях и талантах. Она является одной из основополагающих, а её длина не всегда имеет значение и не увеличивает умственные способности.

О чем расскажет умственная черта

Например, прямая линия Головы указывает на человека с острым умом и нотками хитрости, а если на конце есть разветвление в виде рогатки, то перед вами представитель, соединивший в себе способности к творчеству и точным наукам.

Дополнительный материал по этой теме:

1. Треугольник на линии Ума и его значимость при чтении карты руки.
2. На линии сердца треугольник – еще один хороший знак!

Нить здоровья

Линия Здоровья указывает, насколько человек подвержен различным заболеваниям и как это будет связано с его жизнью. Когда такая линия отсутствует, у человека будет хорошее и стабильное здоровье.

Символ и нить здоровья

Зато, если она слегка касается жизненной линии, то стоит ждать частых недугов. Если человека мучает слабость, усталость, стабильные простуды и проблемы с иммунитетом, то, вероятно, линия Здоровья есть, но слабо выражена.

Треугольники, играющие важную роль в жизни человека

Как мы говорили, треугольник на руке в хиромантии – интересное явление, которое может иметь множество значений и ответов.

Есть роковые знаки, готовые изменить всю судьбу человека

Треугольник на холме луны в хиромантии характерен для людей, которые обычно связаны с чем-то мистическим и духовным, им проще получить такую связь, чем другим. Они имеют возможность создавать уникальные шедевры искусства.

Как быть, если строение не подходит под размер 3×4

Понятно, что если стороны дома не подходят под заданный размер, придётся производить вычисления. Но здесь всё не так уж и сложно. К примеру, необходимо построить здание, размеры которого больше. Тогда можно сделать одну стену длиной 12 м, а вторую − 15 м. В этом случае, пользуясь всё той же теоремой Пифагора и особенностями «египетского треугольника», несложно вычислить необходимую длину диагонали (она же гипотенуза), которая будет равна 19,2 м.

ФОТО: fsks.ruВсе углы разметки под фундамент должны быть идеально прямыми – это аксиома

«Египетский треугольник» − это способ разметки, используемый в строительстве с незапамятных времён. И то, что он и сейчас достаточно популярен, говорит о работоспособности метода. Главное – использовать его на полную, а не обходиться только поверхностными знаниями.

ФОТО: tvoidom-msk.ruЛучше потратить немного больше времени и вывести углы фундамента, чем впоследствии получить массу проблем при строительстве и отделке

Элементы остроугольного треугольника:

Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.

Рис. 4. Остроугольный треугольник и внешний угол

∠ ВСD – внешний угол

Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника

MС – медиана остроугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 6. Остроугольный треугольник и высота остроугольного треугольника

MС – высота остроугольного треугольника

Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.

Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы  пересекаются в точке, которая является центром вписанной окружности.

Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника

MС – биссектриса угла остроугольного треугольника

Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Треугольник

Издавна фигура соотносилась с огнем, горой, камнем, вершиной, отражала связь мира земного и горнего. Перевернутая вершиной вниз фигура олицетворяла древнейшую Великую Богиню, подательницу небесных вод.

В зависимости от положения вершины, изображение означает женское или мужское начало, а две совмещенные фигуры символизируют созидание и творческую силу. Перевернутый треугольник уподоблялся чаше и Святому Граалю, вершиной вверх — сердцу.

Как первейший символ триединства фигура чаще всего отражала небо, землю и между ними человека либо сущность божественную, человеческую, животную.

Треугольник также обозначал мир мертвых, живых и высших сфер.

1. У древних египтян вертикальная сторона треугольника отождествлялась с мужчиной (начало), горизонтальная — с женщиной (середина, хранилище), гипотенуза — с потомством (завершение). В мире богов эти основы продолжения рода представляла триада Озириса, Изиды и Гора. Египтяне считали природой всего сущего и совершенством число три, содержащееся в треугольнике, священное соотношение сторон и гипотенузы которого соответствовало соотношению 3:4:5.
2. В античных Афинах правильный треугольник был посвящен богине знания и мудрости Афине, а также символизировал космос, созидание, абсолют и считался божественным творением. Тетрактис Пифагора, содержащий десять точек и девять равносторонних треугольников, отождествлялся с Великим Единосущным, содержащим в себе все остальное.
3. В христианстве фигура символизирует Троицу и в качестве треугольного нимба является атрибутом Бога-Отца. Так называемый щит Святой Троицы в виде перевернутого треугольника нередко является частью витражей готических соборов. В период Возрождения треугольник с божественным всевидящим Оком изображался как знак высшего проведения, а позже стал частью масонской символики. Глаз Бога, изображенный в треугольнике, также является символом Иеговы в иудаизме и присутствует в культовом изобразительном искусстве Древнего Египта.

Существуют иные фигуры, образующие три равные стороны. Период и места их происхождения отличаются, но в христианстве значение символа триединства для этих знаков остается аналогичным — они все отождествляют Святую Троицу.

Прямоугольный треугольник

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. 

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника. (Рис.14)

Один острый угол прямоугольного треугольника на $44°$ больше другого острого угла. Найдите больший острый угол.

Решение:

В прямоугольном треугольнике $АВС$ $∠А$ и $∠В$ – острые.

Пусть $∠ А – х$, тогда $∠ В — (х+44)$.

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

На основании этого правила, составим и решим уравнение:

$х+х+44=90$

$2х+44=90$

$2х=90-44$

$2х=46$

$х=23$

Угол $В$ больший в этом треугольнике, через $«х»$ он записывался как, $х+44$, следовательно, $∠В=23+44=67°$.

Ответ: $67$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$ 

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. Основное тригонометрическое тождество: $sin^2x+cos^2x=1$
6. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
7. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
8. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Тату треугольник: фото примеры актуального и современного нательного дизайна

Неповторимость татуировки гарантирует обладательнице только свойственную ей индивидуальность и неповторимость. Выбирая тату треугольника по фото, обязательно старайтесь внести что-то свое, личное в нательное изображение. Нельзя сделать татуировку как под копирку

Важно вложить в нее особый смысл, понятный только вам и вашим близким людям. Тем более, что вы знаете о том, что при выборе необходимо основываться на значение тату треугольника и дополнительных орнаментов

Цветовое решение в данной ситуации тоже играет немаловажную роль. Если вы жизнерадостны, то не стоит выбирать сплошное черное тату с треугольником, а лучше внести живые нотки ярких красок в рисунок, который будет сопутствовать с вами по жизни.

их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).

Признаки равенства
треугольников.

Треугольники равны, если у них
соответственно равны:

a) 
две стороны и угол между ними;

b) 
два угла и прилегающая к ним сторона;

c) 
три стороны.

Признаки равенства прямоугольных треугольников. 

Два прямоугольных треугольника равны, если
выполняется одно из следующих условий:

1)  равны их катеты;

2)  катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3)  гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу
другого;

4)  катет и прилежащий острый угол одного треугольника равны катету и
прилежащему острому углу другого;

5)  катет и противолежащий острый угол одного треугольника равны катету и
противолежащему
острому углу другого.

Замечательные линии и точки в
треугольнике.

Высота
треугольника — этоперпендикуляр,опущенный из любой вершины
на противоположную сторону
(
или её продолжение).Эта сторона называетсяоснованием треугольника.Три высотытреугольникавсегдапересекаютсяв одной точке,
называемой ортоцентром треугольника.Ортоцентр остроугольного
треугольника ( точка O,
рис.26 ) расположен внутри треугольника, аортоцентр тупоугольного
треугольника ( точка O,
рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с
вершиной прямого угла.

Медиана
– это отрезок,
соединяющий любую вершину треугольника с серединой противоположной стороны.Три медианы треугольника
(AD,BE,CF,
рис.28 ) пересекаются в
одной точке
O,
всегда лежащей внутри треугольникаиявляющейсяегоцентром тяжести.Эта точка делит каждую
медиану в отношении 2:1, считая от вершины.

Биссектриса
– этоотрезок биссектрисыуглаот вершины доточкипересечения с противоположной
стороной.
Три биссектрисы треугольника
( AD,
BE,
CF,
рис.29 ) пересекаются в
одной точке О, всегда
лежащей внутри треугольникаиявляющейся центром
вписанного круга (см. раздел «Вписанныеи описанные многоугольники»).

Биссектриса делит противоположную
сторону на части, пропорциональные прилегающим сторонам;
например, на  рис.29  AECE
= ABBC
.

Срединный перпендикуляр
– это перпендикуляр,
проведенный из средней
точкиотрезка(стороны).Три срединных перпендикуляра
треугольника АВС
(KO,
MO,
NO,
рис.30
) пересекаются в одной точке О,
являющейся центром

описанного круга
( точки K,
M,
N
– середины сторон треугольника
ABC
).

В остроугольном треугольнике эта точка
лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном
-в середине гипотенузы.
Ортоцентр, центр тяжести, центр описанного и
центр вписанного круга
совпадают только в равностороннем
треугольнике.

Теорема Пифагора. В
прямоугольном треугольнике квадрат длиныгипотенузы равен сумме
квадратов длин катетов.

Доказательство теоремы Пифагора с
очевидностью следует из рис.31.
Рассмотрим прямоугольный треугольник
ABCс катетамиa,
bи гипотенузой
c.

Построим квадрат
AKMB,
используя гипотенузу AB
как сторону. Затемпродолжим стороны
прямоугольного треугольника ABC
так, чтобы получить квадрат
CDEF,
сторона которого равна  a+
b
. Теперь ясно, что площадь
квадрата CDEF
равна (a+b)2.
С
другойстороны,этаплощадь равна суммеплощадейчетырёх прямоугольных
треугольников
иквадрата
AKMB,
то есть

c2
+ 4 ( ab
/ 2 ) = c2
+ 2 ab
,

отсюда, 

c2 +
2 ab =( a + b )2 ,

и окончательно имеем:

c2=  a2
+ b2.

Соотношение сторон в
произвольном треугольнике.

В общем случае ( для произвольного
треугольника ) имеем:

c2= a2
+ b2
– 2ab ·cosC,

где
C
– угол между сторонами  a 
и  b
.  

Алгоритм проведения расчётов

Если все подготовлено, то можно переходить к самим расчётам. Если нужно вычислить площадь поверхности правильной формы, то здесь нет ничего сложного – эти формулы уж точно никто не позабудет.

Без рулетки никакИсточник sv.decorexpro.com

Другое дело, когда стена, пол, потолок имеют сложные очертания. Здесь уже придётся сочетать различные приёмы. То есть поделить комнату на несколько блоков, после чего рассчитать площадь каждого из них. А далее от общей площади вычесть или прибавить их.

Вовсе не обязательно мерить длину стен строго вдоль плинтусов – замер можно проводить в любом удобном месте, если, скажем, мешает мебель. То есть выше, ниже, в середине, главное соблюсти при этом строгую параллель полу и потолку. Никаких диагоналей или наклонов! В противном случае расчёты будут неверными.

При возникновении трудностей можно всегда заручиться поддержкой кого-то из домашних.

Правильная геометрия

Каких-либо сложностей касательно того, как вычислить площадь, здесь нет. В случае простого прямоугольника достаточно замерить всего две стороны и высоту, ведь у такой фигуры противоположные стороны равны. Чтобы убедиться, что комната имеет правильные очертания, достаточно приложить к углам строительный угольник, правда не всегда удаётся получить чёткую картину.

Формула для расчёта прямоугольника известна каждому:

S=a⋅b, где:

• S – рассчитываемая площадь;
• a – длина;
• b – ширина.

Кажется, что формулу площади прямоугольника забыть невозможно, хотя у некоторых получается и этоИсточник wezanu.ritobypus.ru.net

Такая формула актуальна для стен, потолка, пола, дверей, окон и прочих прямоугольных поверхностей

В случае запланированного ремонта важно получить чистые значения. Для этого следует от площади стены вычесть площадь дверей, окон

Общую площадь всей комнаты можно рассчитать по такой формуле – h(a⋅2+b⋅2). Где h – высота помещения.

С квадратом все ещё проще – достаточно замерить одну сторону и возвести её значение в квадрат.

Помещения с неправильными очертаниями

Но как посчитать площадь комнаты, если она имеет неправильную форму поверхностей? Здесь есть некоторые нюансы:

• Стены. В мансардной комнате стена может иметь форму трапеции или треугольника.
• Потолок. В тех же мансардных помещениях данная плоскость может быть под определённым углом. Также есть варианты с ломаной поверхностью, когда несколько плоскостей пересекаются межу собой.

Но ничего страшного здесь нет и не нужно углубляться в тригонометрию. Достаточно любую сложную поверхность стен или потолка визуально разделить на несколько простых плоскостей. После этого остаётся рассчитать площадь каждой фигуры и сложить их вместе.

Случай чуть-чуть посложнее – но не намногоИсточник wezanu.ritobypus.ru.net

Для облегчения ниже приведём несколько формул площадей, которые могут пригодиться:

Круг:

• S=π⋅R² – нужен только радиус.
• Сектор круга определятся так – S=0,5pr.

Параллелограмм:

• S=a⋅b⋅sin(α) – по двум сторонам и углу между ними.
• S=a⋅h – по высоте и основанию.

Треугольник:

• S=0,5⋅b⋅h – по основанию и высоте.
• S=0,5⋅ab⋅sin(α) – по сторонам и углу.
• S=√(p·(p-a)·(p-b)·(p-c)) – формула Герона по трем сторонам.

Трапеция:

• S=0,5⋅h⋅(a+b) – по высоте и основанию.
• S=m⋅h – по средней линии и высоте.

Эллипс:

• S = π⋅R1⋅R2 – по двум радиусам R1 и R2
• S=π⋅a⋅b – через полуоси a и b.

Обозначения: π – 3,14159 (всем известное число пи), R – радиус, a, b, c – стороны фигуры, p – полупериметр (для формулы Герона), h – высота, m – средняя линия.